タイトルの件で、各所で色々議論があるものの、明確な数字等が出ていないような気がしますし、個人的にかなり気になったので計算をしてみました。
目次
背景
現在のALT環境において、マナリアウィッチでの《知恵の光》をマリガン時に単キープすることに関して、いろんな議論があります。
単キープする派の意見
- 1ターン目に《知恵の光》を使うことで、デッキを圧縮して欲しいマナリアカード(アン、ミラ、オーウェンあたり)を引きやすくする
- 同上で、次のターンで動ける2コストカードを引いてくる
- スペルブーストカードが手元にあれば早々にブーストできる
など
マリガンで戻す派の意見
- 初手で1枚引くならマリガンで引くのと同じだから、欲しいマナリアカードなどを引くために0コストでデッキ引けるマリガンで戻すべき
- マリガンで戻してなお、《知恵の光》を引いてきて打てる可能性があるので、こっちの方が分がある
- 《知恵の光》キープした上で《知恵の光》が被ったらテンポ悪くないか?
- そもそもマナリアウィッチはスペルブーストに重きを置くデッキと見ていない
など
議論の争点
前述したような意見の中で、矛盾する意見となっているのがそれぞれの1番になります。
ということで、《知恵の光》を単キープして、デッキ圧縮した方が欲しいカードを引きやすいのか?それともマリガンで全部戻して引きなおした方が引けるのか?を確率論的に計算してみたいと思います。
計算の考え方
全体を通して、「そのターンのドローをするまでに、少なくとも1枚の欲しいカードを引ける確率」を計算してみようと思います。
つまり、計算上は、
1-(欲しいカードが1枚も引けない確率)
で計算できることになります。
そのような考え方で計算をすすめてみます。ちなみに先攻後攻でドロー枚数変わるのが面倒なので、先攻を前提に計算します。
マリガンの考え方
過去の検証等※から、どうやらシャドウバースではマリガンで戻したカードは引きなおしで引いてこない仕様ではないかといわれています。
※ハイランダーデッキでマリガンをたくさん行って、被らなかった結果より(最新の見解があれば教えて欲しいです)
なので、今回はそういう仕様だという前提で計算を行います。
マリガンは初手3枚から任意の枚数をデッキから引きなおすことができます。つまり、《知恵の光》を単キープする場合は、残りのデッキ37枚から2枚を引くことなり、全力マリガンする場合は、残りのデッキ37枚から3枚を引くことになります。
これを式にあらわすと、37枚からX枚(X:マリガンで引きなおす枚数)引きなおす場合の場合の数は、C(37、X)通りとなります。(※Cはコンビネーションの意味)
次に、欲しくないカードを引く場合の数は、欲しくないカードは37-Y枚(Y:欲しいカード枚数)なので、37-Y枚の中からX枚引く場合の数となるので、C(37-Y、X)通り。
つまり、
マリガンで欲しいカードが1枚も引けない確率
=C(37-Y、X)/C(37、X)
となります。
マリガン後の通常時のドロー計算について
これも同じような考え方で計算を行います。
直感的にはデッキの枚数が今○枚だから、あれを引ける確率は○○だ、という考え方になりがちですが、少なくとも1枚引ける確率を計算する場合は、その「今デッキが○枚だ!」の前にすでに1枚以上引いている確率を考慮しなければならないので別の考え方を行う必要があります。
これも先ほどのマリガン時と同じように、デッキの枚数からドローした回数のうち、すべて欲しくないカードを引いた場合の確率を求めることで少なくとも1枚を引く確率を求めることができます。
ドローした回数をZ回とすると、初期手札3枚の時点でデッキは37枚なので、ひけるカードの組み合わせはC(37、Z)通りあることになります。
この中で、欲しくないカードは先ほどと同様に37-Y枚(Y:欲しいカード枚数)なので、37-Y枚の中からZ枚引く場合の数となるので、C(37-Y、Z)通り。
つまり、通常のドローで1枚も欲しいカードが引けない確率は、
=C(37-Y、Z)/C(37、Z)
となります。
マリガンと通常ドローを合算した確率
ということで、これまでの確率から、1-(欲しいカードが1枚も引けない確率)を計算すると、
1-(欲しいカードが1枚も引けない確率)
=1-(マリガンで欲しいカードが1枚も引けない確率)×(通常のドローで1枚も欲しいカードが引けない確率)
となります。
式で言うと、
1-C(37-Y、X)/C(37、X) × C(37-Y、Z)/C(37、Z)
となります。
X:マリガンで戻す枚数
Y:欲しいカードの枚数
Z:ドローした枚数
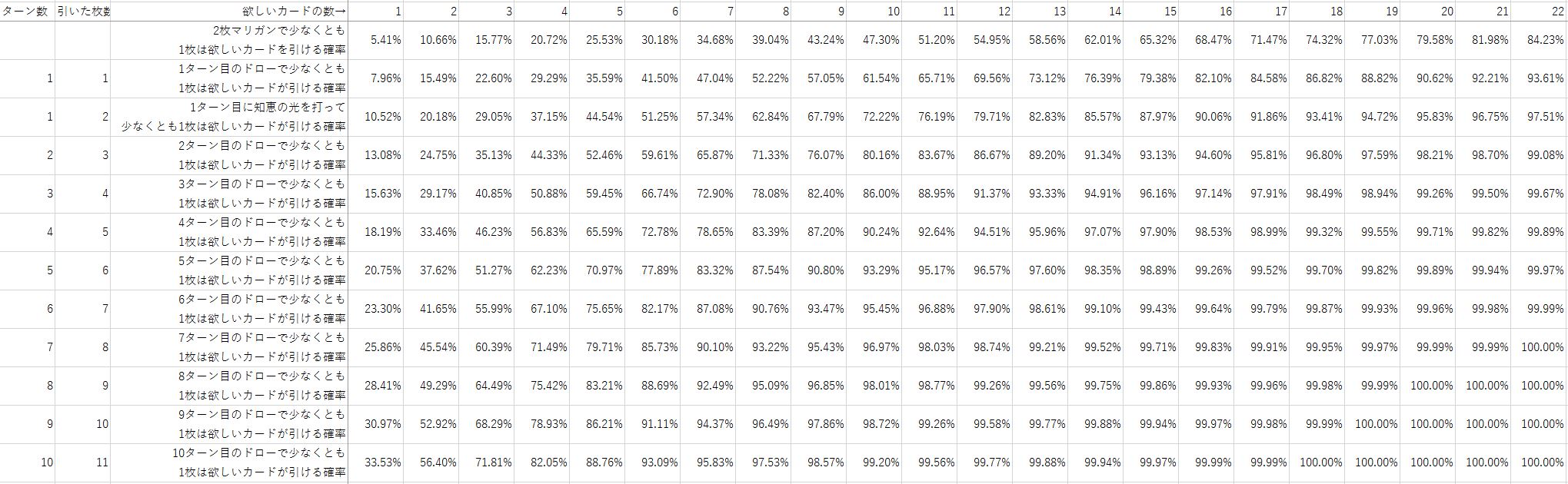
計算結果
ということで、計算した結果がしたの表になります。
《知恵の光》単キープ時(2枚マリガン)
(クリックで大きくなります)
横軸が欲しいカードの数Y、縦軸がドローした枚数Z
3枚マリガン時
(クリックで大きくなります)
横軸が欲しいカードの数Y、縦軸がドローした枚数Z
ユースケースによる比較
上の表だとわかりにくいので、ある1ケースに絞ってみます。
欲しいカードを、ミラ、アン、オーウェンの3種9枚に固定した場合の結果を下記します。
(クリックで大きくなります、念のため計算式もキャプチャしたので間違い等に気づいた方は指摘お願いします)
考察
この結果を見ると、《知恵の光》を単キープして1ターン目に《知恵の光》を打ったときのみ、全マリガンを0.3%ほど上回りますが、それ以外は総じて全マリガンのほうが少なくとも1枚欲しいカードを引ける確率が高いです。
つまり、少なくとも1枚は欲しいカードが引きたい!という場合は、ほとんどの場合、全力でマリガンしたほうが確率としては高いということになります。しかも、《知恵の光》を返した結果、別の《知恵の光》がやってくる可能性があるというおまけ付です。
デッキ圧縮という考え方では、もちろん《知恵の光》を初手で打った方が有利なのは間違いないと思います(単純にドローしている枚数が多いため)。ただし、マリガンという性質が絡む条件下ではデッキ圧縮効果をうわまわることになる結果となるようです。
どういう条件下でそれが変わるのかは、今回の検討とは別で、検討の余地が残りそうです。
おそらく、今回は「少なくとも1枚引ければよい」という着眼点で計算していましたが、「可能な限りたくさん引きたい」という着眼点ではひょっとしたら結果が異なるのかもしれません。
また、時間があったときに検討してみたいと思います。
(追記:2019/1/5 23:10)計算ミスしていました。結果のエクセル表も差し替えました。
計算ミスしていたので再考察
結論として、3ターン目に逆転するという結果になりました。
つまり、1~2ターン目は全力マリガンしたほうが欲しいカードを引ける確率は高いが、3ターン目以降は《知恵の光》をキープし、プレイしてデッキ圧縮しておいた方が良い、ということのようです。
今回の検討では、全力マリガンする側がマリガンで再度《知恵の光》を引いてきて1ターン目にプレイする可能性を無視しているので、そこを考慮するとどうなるか後日計算してみたいと思います。
(2019/1/6 追記) 計算してみました。
注意点
再三になりますが、確率計算ってとても難しいので(検算ができない)、計算ミス等、考え方の相違等あれば教えてもらえると助かります。