※2019/1/5追記:下記計算結果が間違っているようなきがするので計算式の見直ししようとおもいます。現状はあくまで参考程度にとどめておいて欲しいです。
※2019/1/13追記:全力マリガン時の式を誤っておりましたので、修正しました。
デッキを構築する上で、カードの投入枚数って悩みますよね。
そこで何枚デッキに入れていると何ターン目までに引ける確率はどんなものだ、というのを計算してまとめてみました。
条件はターンの開始時に1枚ドローするという前提です。ですので、1ターン目に記載されている確率というのは、40枚から4枚ドローしたときに、目的のカードが少なくとも1枚引ける確率、という計算になっています。
応用として、ドローカードを使う場合は、そのドロー枚数分見るターン数の段をずらしてもらえればそのまま引ける確率になります。
※計算ミス等あれば教えてください。
確率データ表
50%以上を青字、70%以上を太字にしています。
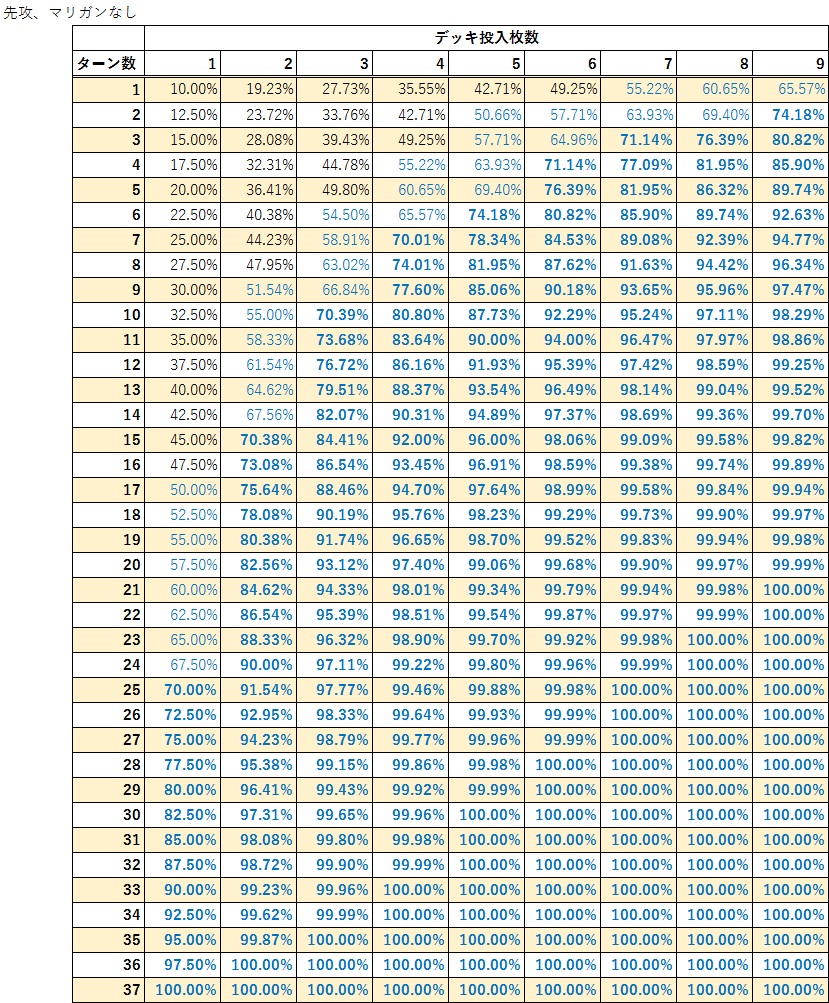
先攻マリガン考慮なし
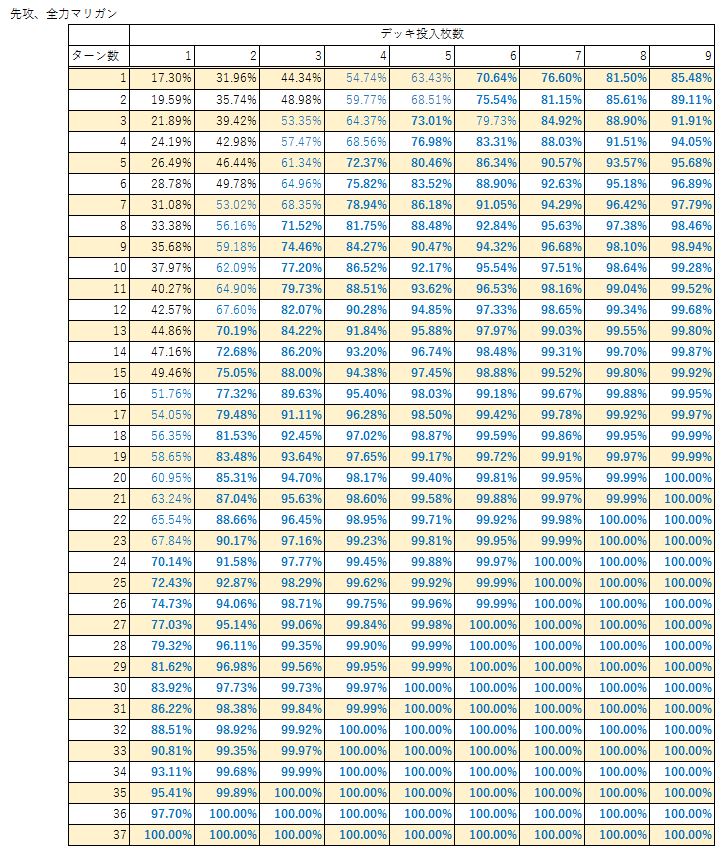
先攻全力マリガン(3枚戻し)
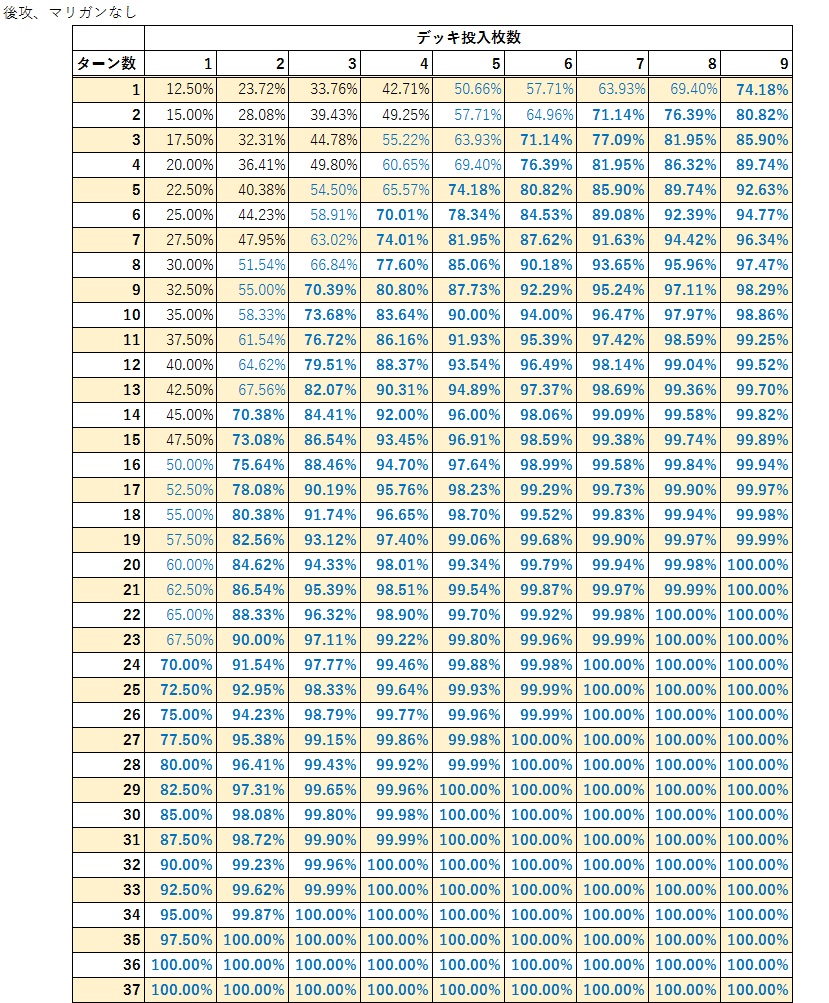
後攻マリガン考慮なし
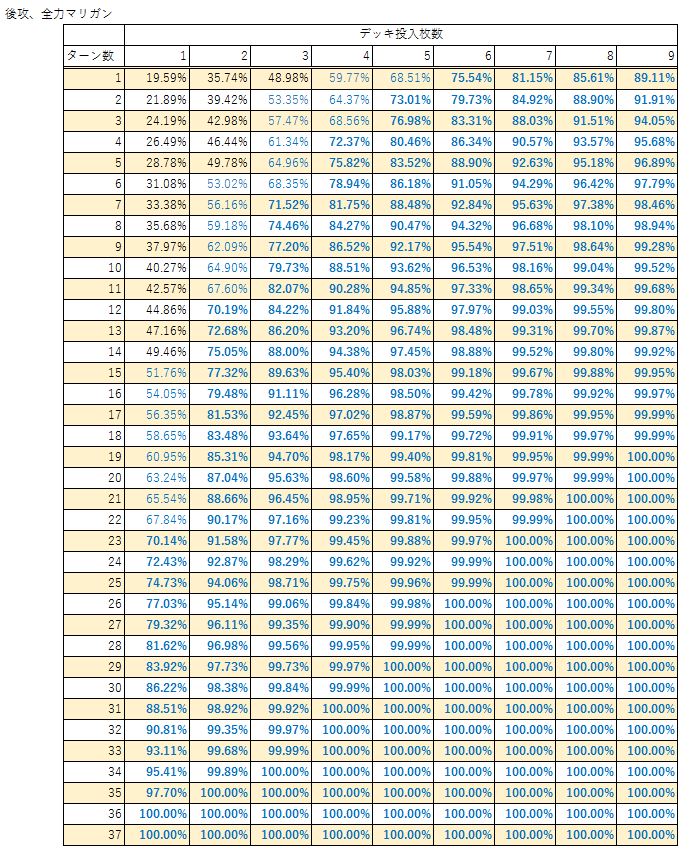
後攻全力マリガン(3枚戻し)
見方の例
たとえば、先攻で1ターン目から60%くらいは動きたいといった場合の1コストの枚数は、8枚ということがこの表からわかります。
あとは、先攻2ターン目に2コストフォロワーを9枚入れて全力マリガンしても89%くらいで、10回に1回くらいは出せないんだなーというのがわかります。
先攻4ターン目までに全力マリガンして《ベルフェゴール》を引ける確率は、57.47%でおよそ半分よりは引けるかなくらい、というのがわかります。(なんとなく体感にも合う気がします)
デッキを組む際に、こういう確率を頭に入れた状態で組むことでデッキの周り具合も把握できますし、マリガンの参考にもなります。
計算式
全力マリガン時の計算式をメモ書き程度に書いておきます。
少なくとも1枚引ける確率
=1-(C(40-X,3)×C(40,3))×(C(37-X,3)×C(37,3))×(C(37-X,Y)×C(37,Y))
X:欲しいカードの投入枚数
Y:ドローした枚数
注意点
個人が勝手にやった計算結果なので間違っている可能性があります。何かおかしいんじゃないかなどあれば連絡してもらえると助かります。