私はこのWUP環境で、戦績を付けることにしました。いろんなデッキを試して、それぞれの勝率が出てきて、「おお、このデッキは勝率いいし絶対強いわww大会で使おうっと^^」みたいなことができるので、楽しんで戦績を付けています。
しかしながら、実際大会で使うと「なんか知らんが事故るな……おかしい、こんなはずではなかったのに」となり、改めてランクマでも使うとやっぱり事故る。つまり、前述の勝率はたまたま上振れていたときに勝ちが重なって、勝率として高く出ていたことになります。
じゃあ、ここで疑問が出てきます。
何戦くらい戦えば、それらしい勝率って出るの?
です。
勝率という言葉は、出てきた結果に対する言葉だと思うので、別に上振れた結果も勝率と言えば勝率です。ここでは、色々ややこしくなるので、言葉の定義として、無限回数試行した結果出てくる最終勝率を「真の勝率」と呼ぶことにします。
また、勝率は環境が変われば変わるものなので、以下考察する内容は、AというデッキのBというデッキに対する勝率、みたいな感じで置き換えてもらったほうがいいかもしれません。
それでは考えてみます。
問題の確認(具体的な簡単なシチュエーションに置き換えます)
シャドバの話をする前に、何が問題なのかを簡単な具体例を示しておさらいしていましょう。
コインを投げて表か裏かが出る問題を考えてみます。
もちろん皆さんご存じの通り、表が出る確率は1/2、裏が出る確率は1/2です。表が出る=勝負に勝つとすると、真の勝率は1/2=50%となります。
では、実際コインを4回投げてみましょう。
1回目:表
2回目:表
3回目:表
4回目:表
4回中4回表が出た(=勝った)ので、勝率100%です!
……あれ?真の勝率50%と全然違う結果になりましたね。
これが、冒頭で述べた上振れによって誤認した真の勝率の問題となります。
もちろん確率なので、こんなことは起こりえます。具体的には表が出る確率は1/2なので、4回連続で表が出る確率は1/2*1/2*1/2*1/2=1/16(=6.25%)です。これぐらいの確率で上のような事象は起こりえます。
ちなみにほかに起こりえる事象は、下記です。
0回表(勝率0%)→1/16(=6.25%)
1回表(勝率25%)→4/16(=25%)
2回表(勝率50%)→6/16(=37.5%)
3回表(勝率75%)→4/16(=25%)
4回表(勝率100%)→1/16(=6.25%)
勝率50%なので、2回表が出る確率が一番高くなっています。とはいえ、37.5%しかないです。多くの場合では、4回という試行では真の勝率を誤認することになります。
これに対する解決策は、試行回数を増やすということです。直感的にもたくさんたくさんコインを投げれば、限りなく50%に収束することはわかると思います。
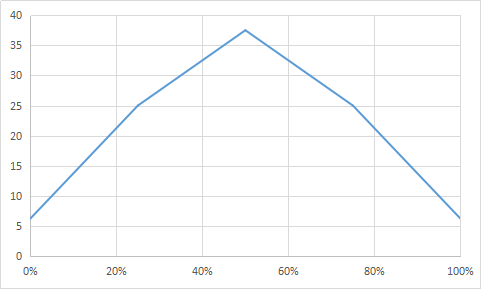
上の結果をグラフに書くとこうです。横軸が、試行した結果得られた勝率で、縦軸はあまり意味はないですが、頻出度くらいに思ってもらえればいいと思います。
これが試行回数を増やすと、
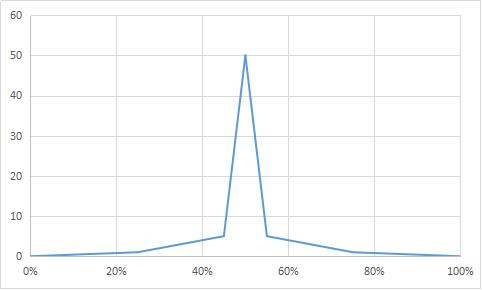
こんな感じで、50%のところが尖がるようになるはず!
ということで、この尖り具合と試行回数の関係について調べてみようと思います。
計算をしてみよう
計算式
細かい計算式を書きます。興味ある方だけ読んでもらえればと思います。
真の勝率P、試行回数n、n回のうちi回勝つ事象が発生する確率は、
nCi * P ^ i * (1-P) ^ (n-i)
で求めることができます。
CはCombinationです。
上のグラフでいうところの、縦軸が上式の計算結果、横軸が i/n %となります。
算出方法
あまり詳しくないのですが、コインを投げて裏表50%の確率でこれまでやってきた議論は、たぶん二項分布とかになるんじゃないかな、と思います。(違っていたらごめんなさい)
そういう理論的なお話があるなら、そこから数式を解けばいいのかもしれませんが、面倒くさいので、プログラミングで力業で解決させます。
上の計算式を使って、iでForループして計算させ、試行回数nを変えていくとどうなるかをグラフを書いて計算してみます。
計算条件としては、真の勝率P=60%と仮置きして計算します。(厳密には真の勝率の値によって計算結果は変わりますが、収束の具合のオーダーまでは変わらないんじゃなかなと思っています)(あと、50%だと詳しい方に二項分布の計算すれば良くね?みたいなつっこみされると悲しくなるのでちょっとずらします)
計算結果
試行回数n=100
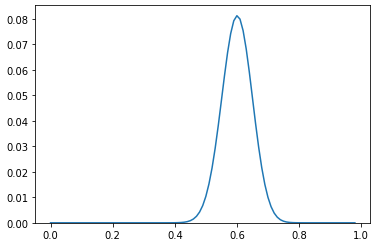
真の勝率60%(=0.6)を中心になだらかの曲線を描いています。
試行回数n=300

ちょっとスリムになってきました。
試行回数n=500
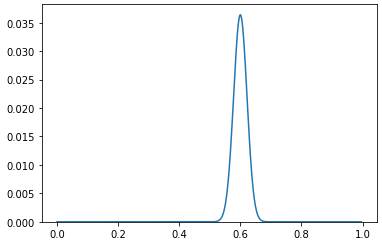
そこそこスリムになってきました。
試行回数n=700
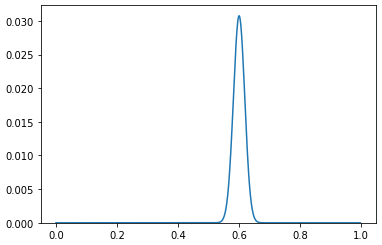
だいぶスリムになってきました
試行回数n=900
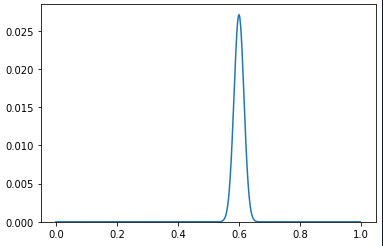
結構スリムになってきました
と、結果はここまでにします。計算機が扱える桁数の都合上、試行回数1000回を超えるあたりからオーバーフロー(10の300乗とかいっちゃう)起こしちゃって計算できませんでした。(かしこいアルゴリズムならできるかも?)
グラフを見ただけだと、「なんとなく100回くらいでも足りなさそうだね」程度しかわからないと思います。
もう少しまとめてみます。
まとめの表
許容誤差範囲が占める割合を下表にまとめます。
| 試行回数 | 許容誤差 ±5% |
許容誤差 ±3% |
許容誤差 ±1% |
| 100 | 0.74 | 0.52 | 0.24 |
| 300 | 0.93 | 0.74 | 0.32 |
| 500 | 0.98 | 0.84 | 0.38 |
| 700 | 0.99 | 0.90 | 0.44 |
| 900 | 0.99 | 0.94 | 0.48 |
これは何を表しているかというと、許容誤差±5%というのは、真の勝率60%に対して誤差5%、つまり55%~65%ですね、この範囲が全体のうちどれくらい占めているかを表しています。
例えば、試行回数100回だと、55%~65%の範囲は、全体の74%ということです。上振れたり下振れたりして、勝率が55%~65%から外れる可能性が残りの26%分くらいある、という意味です。
図解すると下記です。
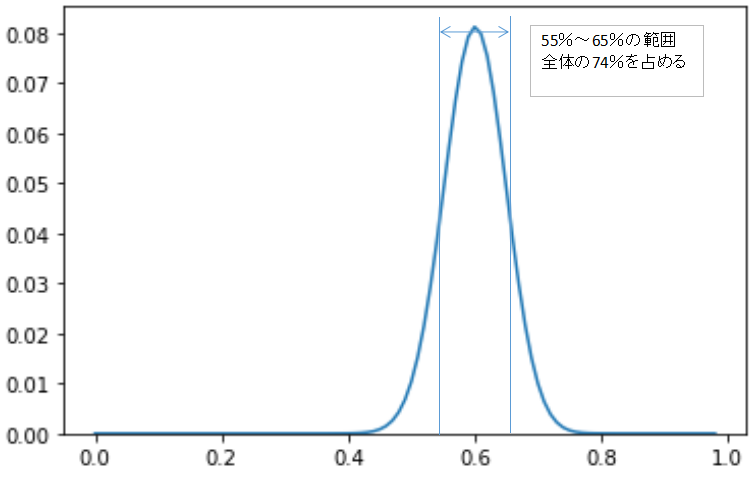
考察とまとめ
表を見ると、±5%くらいの精度で許容するのであれば、300回くらい対戦すれば9割がた真の勝率に近づけそうって感じですね。
また、±1%くらいの精度をめざすなら、900回でも全然足りなさそうです。
感覚的に±5%って緩すぎる気がするので、±3%あたりを狙うとして、500回ぐらいが現実的な数字でしょうか。
マスターランク→グランドマスター0まで勝率60%で行くのがちょうど500戦くらい(連勝ボーナスや格上戦除いて)なので、試行できなくはない回数範囲ですね。
とはいえ、AというデッキとBというデッキの相性確認のために500回、それをあらゆる組み合わせで試す…なんてとてもじゃないですが時間足りない気はしますが。。
今回は単純な確率の上での話をしましたが、実際はプレイングといった人為的要素も入ってくるので、実際はもっと複雑です。
さいごに
最後にまとめると、冒頭のお話に戻りまして、50戦くらいでいい勝率出たからって大会に持ち込んで泣きを見るのものある程度妥当だったな、ということが個人的にわかったので良かったです。